Akkorder og melodier kan gjenskapes som vakre geometriske former. Nye matematiske modeller kan gi innsikt i musikkstiler og la oss se forskjellen på sangene til John Lennon og Paul McCartney, hevder amerikanske forskere.
Denne artikkelen er over ti år gammel og kan inneholde utdatert informasjon.
Ved å bruke dyp, kompleks geometri har forskerne laget modeller som kan brukes til å forstå hvordan harmonier og melodier er bygget opp. I en artikkel i tidsskriftet Science kaller de metoden ”geometrisk musikkteori”.
Med denne teorien kan forskerne analysere musikk på en ny måte.
- Det mest tilfredstillende med forskningen at vi nå kan se en logisk struktur som binder sammen mange, mange forskjellige musikalske begreper, sier en av forskerne, Dimitri Tymoczko fra Princeton-universitetet i en pressemelding.
- Til en viss grad kan vi framstille musikkhistorien som en lang prosess gjennom å utforske forskjellige symmetrier og geometrier, fortsetter han.
"Kulene er treklang-akkorder. Den røde kula symboliserer akkorden der tonene er fordelt med lengst mulig og dermed lik avstand fra hverandre utover i en oktav. De blå kulene tilsvarer den motsatte ytterligheten: Akkorder bestående av tre identiske toner klumpet oppå hverandre."
Forskjellen på Lennon og McCartney
Det matematiske verktøyet kan også brukes til å finne forskjeller mellom musikalske stilarter.
- Våre metoder kan gjøre det mulig å se noen av forskjellene mellom John Lennon og Paul McCartney, sier Tymoczko.
- Og de kan helt sikkert hjelpe oss å få en dypere forståelse for hvordan klassisk musikk forholder seg til rock eller er forskjellig fra atonal musikk, sier han.
Forskerne har først og fremst analysert vestlig musikk, fordi denne har akkorder som egner seg bedre for analyse.
Kanskje vil verktøyet også kunne brukes til å finne fram til nye og hittil uhørte akkorder og toneskalaer.
"Dette Möbiusbåndet er en figur med uendelig antall dimensjoner projisert ned i våre tre rom-dimensjoner. Kulene på overflaten er akkorder."
Mangedimensjonal skjønnhet
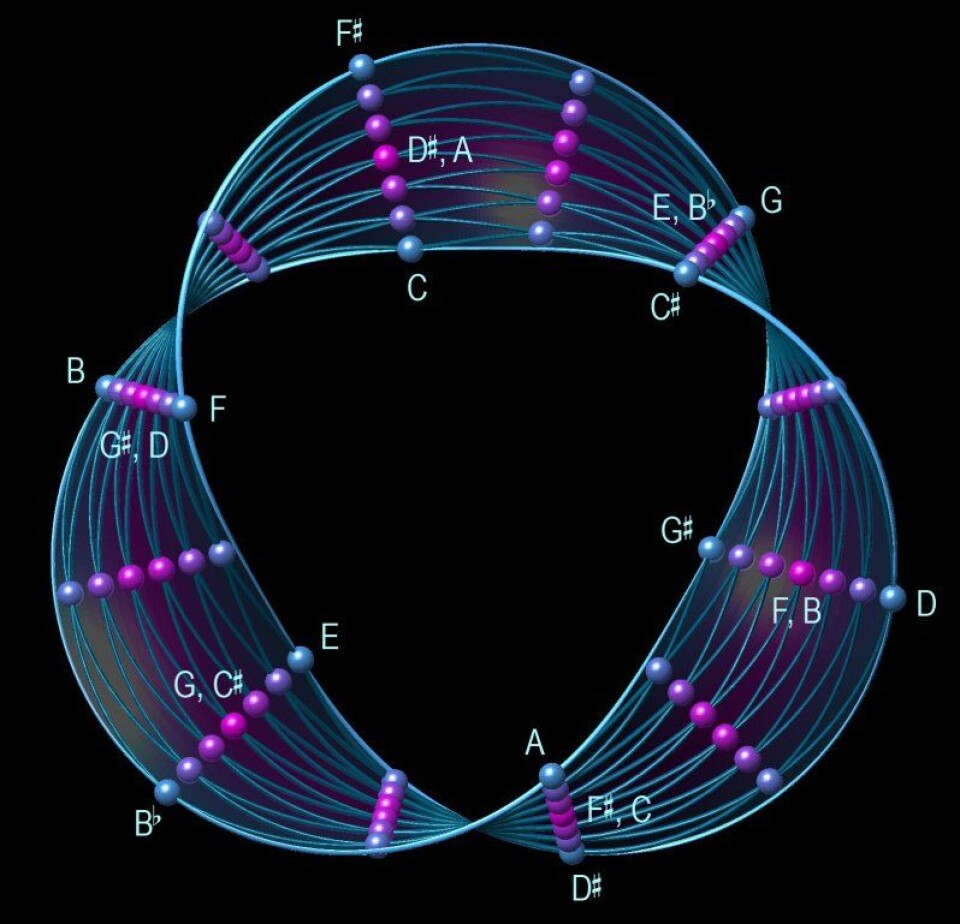
Man må ikke være matematiker for å se det vakre i modellene. En samling med akkorder bestående av fire toner legger seg som fargepunkter rundt et foldet Möbiusbånd.
Denne spesielle geometriske formen har den merkelige egenskapen at den bare har én flate, fordi den folder seg tilbake i seg selv.
Du kan selv lage et Möbiusbånd ved å klippe ut en papirstrimmel, vri enden en halv gang rundt og lime endestykkene sammen.
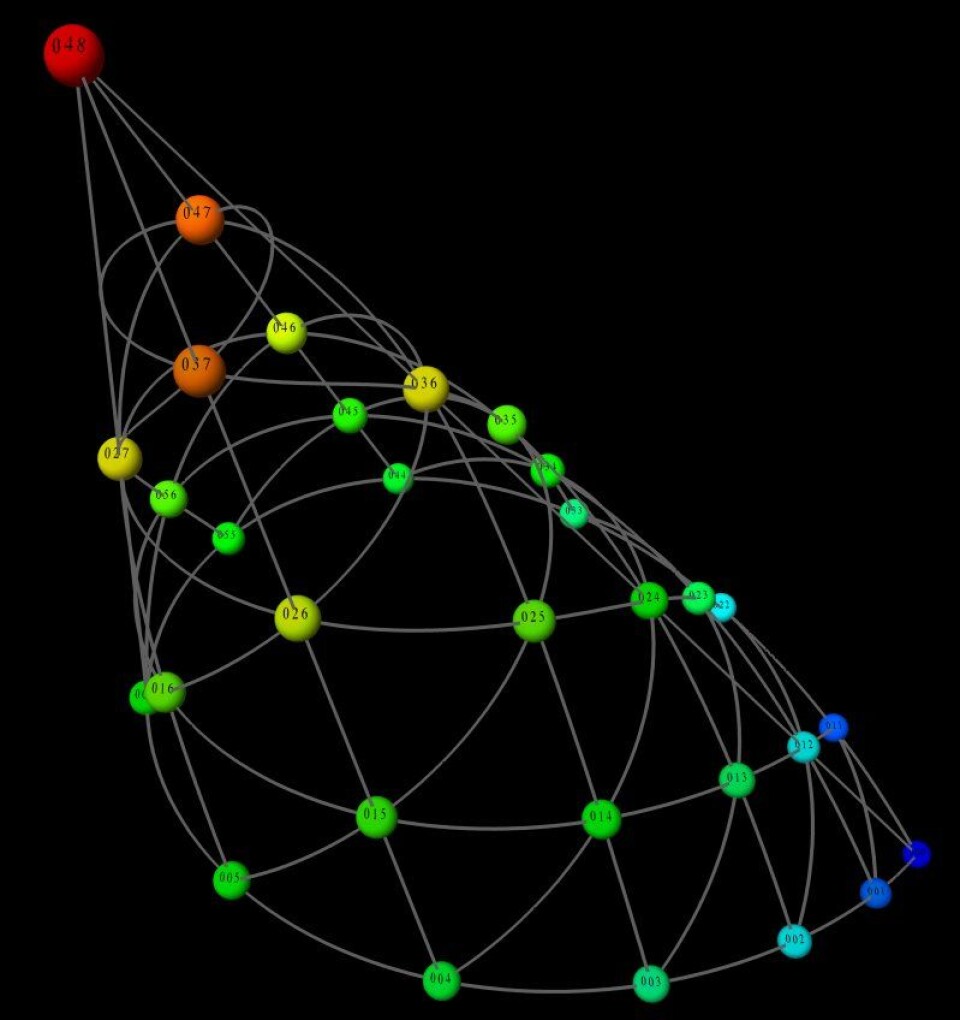
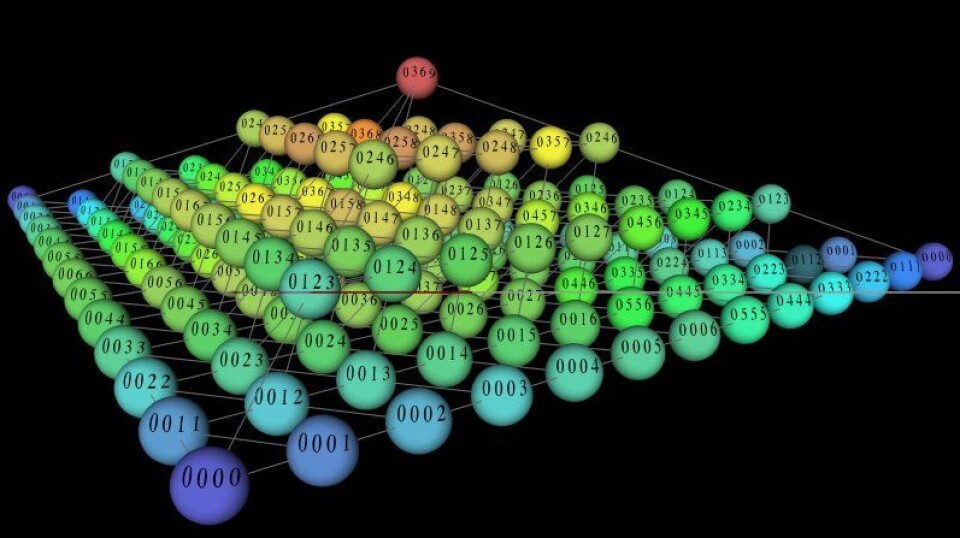
Andre modeller viser akkordene som punkter på en pyramide. Denne pyramiden er egentlig en kegle i et rom med mange flere dimensjoner enn vi kan oppfatte.
Akkurat som når vi ser en perspektivtegning på et flatt ark, kan vi nemlig projisere slike mangedimensjonale figurer ned i våre tre romlige dimensjoner.
Annonse
"Figuren viser akkorder med fire toner. Pyramiden er egentlig en kjegle projisert ned i våre tre dimensjoner. Den røde kula øverst representerer en forminsket septim, som deler opp en oktav i like store intervaller. De blå kulene representerer akkorder der tonene er klumpet tettere sammen på klaviaturet."
Musikk og matematikk
Musikk og matematikk har i over to tusen år hatt glede av hverandre. Matematikeren Pytagoras oppdaget at svingetakten til tonene i vakre klanger står i et enkelt forhold til hverandre.
Naturtonerekka i seljefløyter og bukkehorn framkommer ved at frekvensen i en grunntone multipliseres med hele tall.
I middelalderen ble idéen unnfanget om at planetene beveget seg i perfekte sirkler med størrelsesforhold som tilsvarte vakre harmonier: sfærenes musikk.
Nye musikalske sfærer
Disse idéene om guddommelig perfekte kuleformer var også en hodepine for Johannes Kepler og andre astronomer som etter hvert motvillig måtte innrømme at planetbanene slingret betydelig i valsen omkring sola.
Nå har forskerne gjenskapt drømmen om sfærenes musikk i nye matematiske dimensjoner, bokstavelig talt.
- Sfærenes musikk er ikke egentlig en metafor, sier Tymoczko.
- Noen av de musikalske romlige figurene er virkelig sfærer eller kuler.
Referanse:
Clifton Callender, Ian Quinn, Dmitri Tymoczko: Generalized Voice-Leading Spaces. Science, 14. april 2008.
