Sant, ikke sant?
Jeg kan beskrive virkeligheten i dagligspråk, men mestrer ikke matematiske formler. Er formlene sannere?
Denne artikkelen er over ti år gammel og kan inneholde utdatert informasjon.
– Det er altfor mange her til lands som har angst for matematikk, sier kunnskapsminister Kristin Halvorsen i en nettartikkel fra TV2.
Angst er en vond følelse å ha. Stilt overfor angst, kan du kjempe eller resignere.
Du kan kjempe ved å latterliggjøre fienden: Matte er livsfjernt og unyttig, leketøy for nerder.
Eller du kan kjempe ved å gjøre fienden truende: Matte er kaldt, og brukes av beregnende teknologer til å lage umenneskelige maskiner.
Eller du kan resignere ved å forfremme fienden til en galakse langt, langt borte: Matte er så avansert at det er hinsides hva jeg kan håpe å forstå.
Men langt der borte, i den nerdete galaksen, slumrer likevel matten: Dødsstjernen med den konsentrerte, rene tankestrålen.
Det 21. århundre kan ikke klare seg uten matte. Matten slår tilbake.
Bunsen-baronen og lurium-fantomet
Den gale professor med mirakuløs allmakt står sterkere i klisjéenes verden enn hva godt er. Riktignok heter han ikke lenger dr. Kuppelknas og har blankpolert, tårnende skalle som i min barndoms tegneserier.
Men han er fortsatt like mektig når han mønstrer 120 millioner watt og mange ganger flere euro i jakten på The Goddamn Particle, Higgs-bosonet.
Skal jeg forstå Higgs-bosonet, har jeg to valg. Jeg kan enten godta de populære forklaringene, som ikke forklarer noe som helst: Higgs-bosonet har et korresponderende Higgs-felt, som interagerer med noen partikler og gir dem masse.
Javel. For min del kunne det likegodt stått: Bunsen-baronen er et lurium-fantom som vekselvirker med noen poljetter og gir dem myse.
For hvorfor må partiklene absolutt få masse annet steds fra? Kunne de ikke hatt det fra starten, hvor nå den er? Og hvorfor bare noen partikler, og ikke alle? Og hvordan kan en partikkel finnes hvis den ikke har masse? Og hva slags korrespondanse er det Higgsbosonet fører med Higgsfeltet?
Denne populære forklaringen ender resignert med replikken fra Trond Kirkvaags geniale sketsj: ”Det bare er sånn”.
Slag under brøkstreken
Derfor kan jeg isteden velge å slå opp i Wikipedia. Da skal jeg ikke scrolle langt før de første matematiske formlene hopper rett i fjeset på meg.
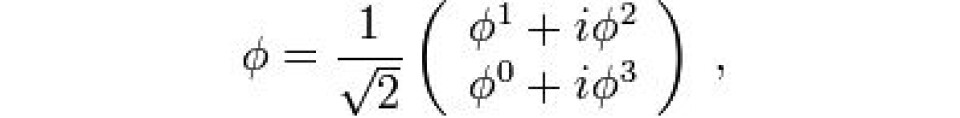
- sier den første, truende.
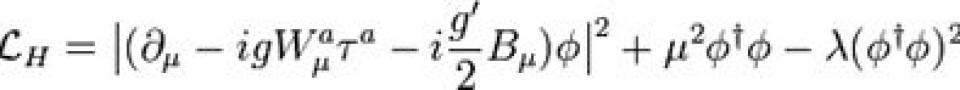
- mumler den andre mørkt. Men mitt vaklende intellektuelle ego går først i bakken etter denne siste, hardtslående Yukawa-interaksjonen:
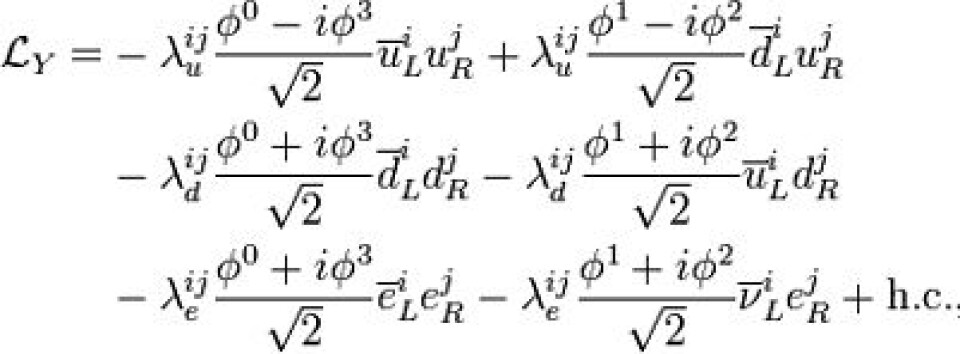
Omtåket av denne ubegripelighet resignerer jeg: Noen har sett sannheten. Og jeg vil aldri begripe den. Men jeg godtar både Large Hadron Collider til milliarder av euro og behovet for å finne en partikkel jeg aldri vil forstå.
Dumme journalister, vil noen kommentere. Og det kan de gjerne få lov til. Faget mitt er å gi folk ord, lyd og bilder som fenger dem, ikke å forstå bosoner og formler.

O Store Higgs
Men heldigvis er det mer skolerte folk enn meg som føler seg dumme. Les hva geologen Daniel Sarewitz skriver i en kommentar i siste utgave av Nature:
De fleste mennesker, inkludert de fleste forskere, kan skaffe seg kunnskap om Higgs-bosonet bare gjennom meteforene og analogiene som fysikere og forskningsskribenter bruker for å forsøke å forklare fenomener som bare virkelig kan karakteriseres matematisk.
Kommentaren fortsetter med en interessant og viktig påstand:
For oss som ikke kan følge matematikken, er det å mene at Higgs-bosonet finnes en troshandling, ikke en rasjonell handling.
Og det er her den dumme journalisten drister seg til å være uenig.
Ikke uenig i at vi lekfolk er henvist til å tro på de populære forklaringene. Heller ikke i at matematikken karakteriserer Higgs-bosonet mer rasjonelt.
Men jeg er uenig i at rasjonaliteten, som matematikken uttrykker mest presist, ikke også er en troshandling.
Newton per pedal
Jeg vil bruke et enkelt eksempel fra matte jeg faktisk forstår, for å forklare hva jeg mener.
I sommer syklet jeg gjennom Europa på et gammelt pedaløk, tunglastet med telt og tasker. Hver gang jeg skulle fortsette etter en pause i veigrøfta, måtte jeg tråkke hardt. Mye hardere enn om jeg hadde brukt min lette, sportslige treningssykkel av aluminium hjemme.
Sagt i hverdagsspråk: Vil du akselerere, så må du bruke mer kraft jo mer masse du har.
Eller sagt på matematisk i den enkleste utgaven av Newtons andre lov:
Akselerasjon = Kraft / Masse.
Drøftet i sin enkelhet: Mer masse under brøkstreken krever mer kraft over, hvis du vil ha samme akselerasjon.
”Det bare er sånn”

Matteversjonen er mer presis og kortfattet. Den kan også brukes til å regne ut akselerasjonen, hvis du kjenner kraften og massen. Men er den sannere? Hviler den mindre på en troshandling?
For hva er egentlig akselerasjon? Fartsendring per sekund, vil fysikeren si. Men hva er sekund? Et mål på et tidsintervall, vil fysikeren si. Og hva er så tid? Hmmm ….
Partisekretær Nikita Khrusjtsjov i det ateistiske Sovjetunionen sa det så kjekt i en tale til sentralkomitéen i kommunistpartiet: ”Gagarin fløy ut i rommet, men så ingen gud der”.
Jeg kan med like stor rett si: Jeg tråkket det gamle pedaldroget til senestrekken tok meg, men jeg så ingen akselerasjon, bare gress og asfalt.
For akselerasjon er en abstraksjon, bygget på idéer som mennesket har dannet seg, fordi de er nyttige til å beskrive og mestre virkeligheten. I matematikken hviler disse abstraksjonene på såkalt selvinnlysende utsagn, aksiomer som ikke kan bevises.
Med andre ord: ”Det bare er sånn.” Og vi er like langt.
Sant, ikke sant
Drømmen om et sannere språk er gammel. Den slynger seg som et standhaftig pennestrøk gjennom skriftspråkenes historie, fra biskop John Wilkins universelle språk via Gottfried Leibniz algebra som skulle kunne uttrykke enhver tanke.
Så ender den i Whitehead og Russells Principa Mathematica, et byggverk der spir over spir av matematisk-logiske utledninger skulle hvile trygt på en urokkelig teoretisk grunnmur.
Det måtte en Kurt Gödel til for å vise hvordan byggverket kunne rive seg selv. Siden har drømmen om det absolutt sanne språk ligget i ruiner.
Higgs i jungelen
Daniel Sarewitz skriver også noe om dette. Kommentaren hans ble til etter et besøk i ruinbyen Angkor i Kambodsja.

Her, i det enorme tempelet i urskogen, grublet han over Higgsbosonet. Og han setter opp en interessant motsetning.
Arkitektene bak Angkor-tempelet har formet bygningene for å gi en fornemmelse av universell orden.
Formen speiler funksjonen, med ornamenter som skal gi en kraftfull følelse av mysterium og overskridende opplevelse, av fruktbarheten i menneskets fantasi og ambisjon i et univers så enormt at logikken unnviker forståelse.
Arkitektene bak byggverket som skal avsløre hemmelighetene til Higgs-bosonet har tenkt annerledes.
Hvis noen om tusen år besøker ruinene av Large Hadron Collider (…), er det tvilsomt om de ut fra restene av detektorene og de superledende magnetene vil få en opplevelse av den subatomiske verden som forskerne sier at den avslører, skriver Sarewitz.
Sinusdansen
Da jeg for mange år siden lærte matematikk, var jeg besatt av å forstå, ikke bare pugge. Jeg ville, for å sitere Einstein, danse til en mystisk melodi, danse til funksjonskurvene, sanse våren eksplodere som den deriverte av årstidenes sinuskurve.
Kanskje kommer matteangsten av at skoleundervisningen sjelden lar elevene se skjønnheten, poesien, det enkle og kraftfulle uttrykket i selv enkle matematiske funksjoner, slik Daniel Sarewitz så den kosmiske skjønnheten i Angkor-tempelet?
Er det matematisk understøttede fysiske verdensbilde i ferd med å miste sin beskrivende kraft? Ikke fordi de intrikate formlene er feil, men fordi det matematiske språket fjerner seg fra poesi henimot bokholderi?
Eller er det fortsatt noen som ser de store, vakre helhetene, men er ute av stand til å kommunisere dem? Hvor er fysikere og matematikere med samme drøm som arkitektene bak Angkor-tempelet? Jeg vil gjerne høre fra dere!
SE OGSÅ
-

– Biologer forstår ikke sine egne metoder
-

Ser matteangst i hjernen
-

Hetta av matte? - Hopp i det
-
Tall kan temmes
-
6 av 10 har matteangst
-
Kan mer om former enn om tall
-

Lær matematikk av skogen
-

- Effektiv metode for mattelæring brukes lite
-

Ønsker flere idealistiske fysikere
-

Vitenskapsmenn – ikke filosofer
-

I Abelrommet med John Tate




























